光线求交
首先实现了不同几何类与光线的求交点算法
使用光线的参数表示
$$ P(t)=R_0+tR_d $$
注意距离 #$t#$ 并非真实单位距离,而是与 #$R_d#$ 相匹配的 #$t#$,归一化 #$R_d#$ 时要避免影响
交点处法向量应与光线方向 #$R_d#$ 成钝角
平面
隐式表示平面为
$$ nP+D=0 $$
则点到平面距离为
$$ t=-(D+n\cdot R_0)/(n\cdot R_d) $$
验算是否满足
$$ t>0 $$
其中平面法向量即为
$$ n $$
三角形
用顶点表示三角形为
$$ P_0,P_1, P_2 $$
设光线与三角形平面交点
$$ P=(1-\beta-\gamma)P_0+\beta P_1+\gamma P_2 $$
令
$$ E_1=P_0-P_1 $$
$$ E_2=P_0-P_2 $$
$$ S=P_0-R_0 $$
则有
$$ \left( \begin{array}{c} t \\ \beta \\ \gamma \end{array} \right) = \frac{1}{det(R_d,E_1,E_2)} \left( \begin{array}{c} det(S,E_1,E_2) \\ det(R_d,S,E_2) \\ det(R_d,E_1,S) \end{array} \right) $$
验算是否满足
$$ t>0 $$
$$ 0\le\beta,\gamma\le 1 $$
$$ \beta+ \gamma\le 1 $$
其中三角形法向量为
$$ E1\times E2 $$
球体
用隐式方程表示球体为
$$ |P-P_c|-r=0 $$
由光源指向球心的向量
$$ l=P_c-R_0 $$
从而可以通过 #$l^2#$ 与 #$r^2#$ 大小关系判断光源是否位于球体内部
球心到光线所在直线的投影点
$$ t_p=l\cdot R_d $$
验算是否光源在球体内部或
$$ t_p>0 $$
球心到光线所在直线的距离
$$ d^2=l^2-{t_p}^2 $$
验算是否满足
$$ d \le r $$
投影点到光线与球面的距离
$$ t_0=r^2-d^2 $$
如果光源在球体外部则
$$ t=t_p-t_0 $$
如果在内部则
$$ t=t_p+t_0 $$
其中球体交点处法向量为
$$ P_c-P(t) $$
相机模型
透视相机
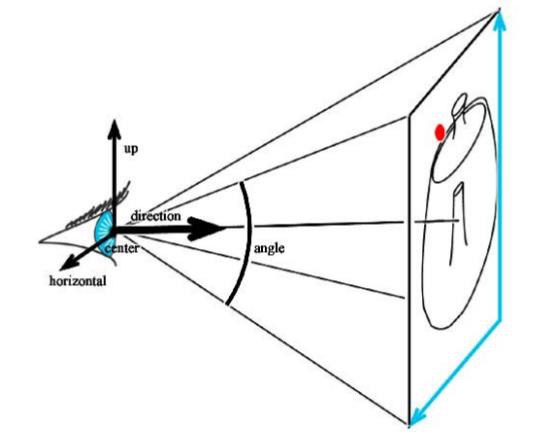
为了计算图片空间射线,使用相机空间变换
空间缩放系数
$$ f_x=f_y=\frac{width}{2\tan(angle/2)} $$
相机空间下射线
$$ d_{R_c}=(\frac{u-c_x}{f_x},\frac{v-c_y}{f_y}, 1)^T $$
其中 #$u#$, #$v#$ 为像素坐标
#$c_x#$, #$c_y#$ 为相机位置,一般取图像中心即 #$width/2#$, #$height/2#$
坐标变换得到
$$ R_d=Rd_{R_c} $$
其中过渡矩阵
$$ R=[horizontal,-up,direction] $$
模型着色
Phong 模型
使用 Phong 模型计算局部光强
$$ I_{pixel}=c_\alpha k_\alpha+\sum_x{c_x(k_dReLu(L_x \cdot N)+k_s{ReLu(V\cdot R_x)}^s)} $$
其中 #$c_x#$ 为光源颜色,不考虑环境光时 #$c_\alpha=k_\alpha=0#$,#$k_d#$, #$k_\alpha#$ 为材质属性
#$N#$ 为相机到相交处的法向量,#$L_x#$ 为相交处到光源的方向向量,#$V#$ 为光线方向
$$ ReLu(x)=\max(0,x) $$
反射光线方向
$$ R_x=2(L_x \cdot N)N-L_x $$
图片处理
从文件中读取配置文件,循环像素点分别计算相机出射光线是否和场景有交点:找到最近交点后叠加来自所有光源的光强影响并累加局部光强,若不存在交点则返回背景色。